What are the chances?
I'm working on a short story about probability, and how people react to extremely improbable events, specifically a coin
which always comes up heads. Basic probability tells us that the chances that a coin will be tossed heads N times in a
row goes down exponentially has N increases, but I wanted to get a better sense of what that really
meant.
I wanted to know: how many times in a row does a coin have to come up heads for you to call it extremely improbable? I decided "extremely improbable" would mean, "If you flipped a coin every second for an entire lifetime, you'd only have a 50% chance of seeing it happen."
My first step was to determine the probability of seeing N heads flips in a row, given that you flipped M coins. I came up with a pair of mutually recursive equations which describe this. One gives the number of sequences of length M containing a subsequence of N heads results in a row, the other gives the number of sequences of length M which don't.
I'm too lazy to justify it here, but I verified it against a brute-force approach for M and N up to 15, and it works. Figuring out why it works is an exercise left to the reader.
I wrote a dynamic programming algorithm to compute this in Go, and with a little bit of work, I got my answer:
If you flip a coin every second for 108 years (a very generous lifetime), you have about a 50% chance of ever seeing the coin come up heads 31 times in a row. To get 10 headses in a row with 50% probability, you only need 1,421 flips (about 24 minutes at one flip per second) . To get 31 you need about 3.4 billion.
Only 31 flips. I think that's remarkable.
I wanted to know: how many times in a row does a coin have to come up heads for you to call it extremely improbable? I decided "extremely improbable" would mean, "If you flipped a coin every second for an entire lifetime, you'd only have a 50% chance of seeing it happen."
My first step was to determine the probability of seeing N heads flips in a row, given that you flipped M coins. I came up with a pair of mutually recursive equations which describe this. One gives the number of sequences of length M containing a subsequence of N heads results in a row, the other gives the number of sequences of length M which don't.
I'm too lazy to justify it here, but I verified it against a brute-force approach for M and N up to 15, and it works. Figuring out why it works is an exercise left to the reader.
I wrote a dynamic programming algorithm to compute this in Go, and with a little bit of work, I got my answer:
If you flip a coin every second for 108 years (a very generous lifetime), you have about a 50% chance of ever seeing the coin come up heads 31 times in a row. To get 10 headses in a row with 50% probability, you only need 1,421 flips (about 24 minutes at one flip per second) . To get 31 you need about 3.4 billion.
Only 31 flips. I think that's remarkable.
.gif)
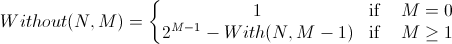.gif)